Random Point In a Triangle – Barycentric Coordinates

A real quick lesson on Barycentric Coordinates.  No diagrams right now.  Maybe I’ll come back later and elaborate.  I’m really going to gloss over the details here – just explain how to accomplish the task in a straightforward manner.

So, you want to find the coordinates of a random point in space that exists on the surface of a predefined triangle.  Sounds complicated, but it’s actually not that bad.  We start off like this:

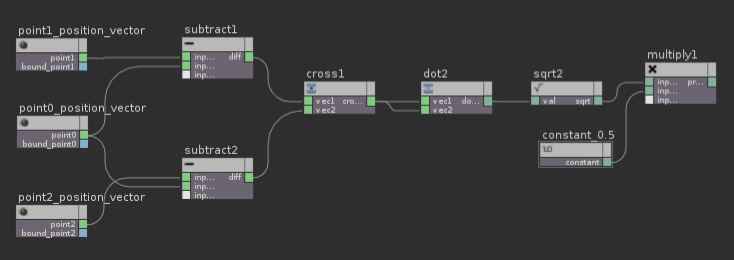
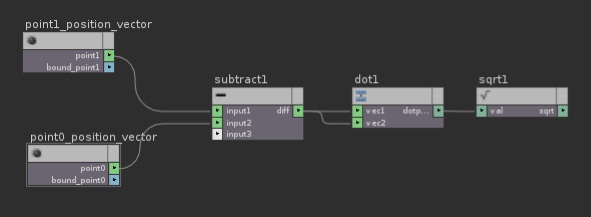
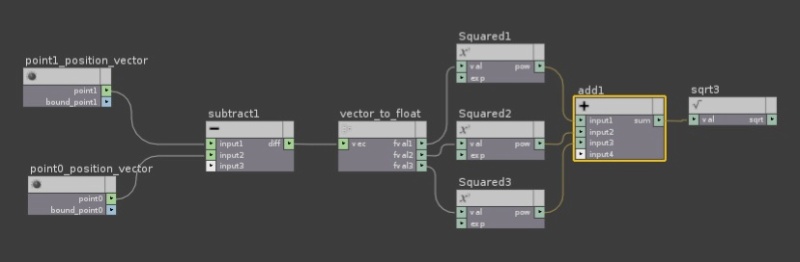
Consider a triangle with points ABC.  Pick any point and then calculate the vectors from that point to the other two points in the triangle.  So, we get vectors AB and AC.  AB = [Bx – Ax, By – Ay, Bz – Az] and AC = [Cx – Ax, Cy – Ay, Cz – Az].

So we now have two vectors that tell how how to get from point A to the other two points in the triangle.  They tell us what direction to go in and how far.

So, what if we start at point A, go a random percentage along the AB vector, then go another random percentage along the AC vector?  Sounds pretty good, but how do we make sure we stay inside the triangle and don’t exceed our bounds?  This is where Barycentric Coordinates come into play.

Barycentric coordinates are three numbers that add up to one.  Each number stands for a weighting of each point of the triangle.  You can think of 1 as a percentage of the triangle. 1 = 100%.  So, if we say point R weights the triangle 30% and S 50% then T is 20%.  Well, knowing all this doesn’t help us that much right now, except for the concept that R + S + T = 1.  Going over 1 means we are outside the bounds of our triangle.  And, a value of R = 1/3, S = 1/3, T=1/3 means each point has equal weighting, something called the barycenter of our triangle.

Consider a unit triangle in two dimensions.  The point coordinates would be [0,0,], [0, 1], [1,0].  Imagine this as the perfect triangle.  We can also think of this triangle in relation to our 3D triangle, with [0,0] representing our point A.  In other words we can remap the values of one triangle to another, or use these barycentric weightings to weight our distance vectors accordingly.

We’ll simply start by choosing two numbers at random between 0 and 1.  Each number should be seeded differently to make sure we don’t end up with the same number.

Now, we need to check if they are larger than one, since we still need to account for the third number and want to make sure we stay inside our triangle.  If they are, all we have to do is subtract them from one.  Something like this:

R = random.Get01(); //Generate a random number called R between 0-1

S = random.Get01(); //Generate a random number called S between 0-1

if(R + S >=1)
{
R = 1 – R;
S = 1 – S;
}

Great, we have our barycentric coordinates. Now, let’s apply them.

Starting at point A, we want to go a random percentage along vector AB, then go another random percentage along vector AC. Our math will look something like this:

RandomPointPosition = A + R*AB + S*AC

Done!

Cross Products

I won’t get into much detail here other than to talk about a few example of why you would want to calculate vector cross products and briefly explain what they are. Wikipedia has a great entry on them which will explain all the math behind them.

Given two vectors, for instance, two sides of a triangle, the cross product will give you a vector that points perpendicular to those vectors.  This has many uses in 3D animation. You can calculate surface area (1/2 the magnitude of the cross product of vectors of two sides of a triangle will give you the area of that triangle). You can calculate surface normals, which show which direction the polygons of your surface are pointing.  You can use cross products to align sprites to the camera or cull geometry that is pointing away from the camera.  One thing I used cross products for recently was in a particle setup where I needed to create an aura around a character.  I was able to figure out which surfaces of the geometry were pointing perpendicular to the camera and use that as a basis for particle emission.  So, many uses.

Area of a triangle in 3D space

It can be very helpful to know how to calculate the area of triangles in 3D space. You can use it to calculate the surface area of an object, which in turn you can use to calculate/set mass or density of objects.  Primarily, I use area to create distribution attributes for particle emission, such that polygons of varying size emit a spatially consistent amount of particles.  For example, in Houdini, if area is assigned as a primitive attribute (you have measured the area of each polygon and stored it) you simply multiply area by emission rate and will get a fairly even distribution of particles emitted from a surface.  Of course, Houdini has a built in operator to calculate area, but if you don’t have such an operator in your 3D program, or you are writing your own code, here’s how to do it.

The main tools needed to calculate an area of a triangle in 3D space are covered in my post about distance.

The basic formula using vectors goes something like this:

Given three vector points in space, A, B, and C, the area of the triangle formed by those points is 1/2 the magnitude (see distance) of the cross product (see cross product) of vector AB and AC.

It can be written in mathematical notation like this:

1/2 * |AB x AC|

It can also be explained diagrammatically like so:

So, given three points, A, B, and C, pick one point arbitrarily and calculate two distance vectors between that point and the other two points (distance vectors AB and AC) by doing vector subtraction.  Find the cross product between those vectors.  The cross product outputs a vector.  Now, calculate the magnitude of this vector, and finally divide by 2 (or multiply by 0.5).

Distance or Magnitude of Vectors

I’ll briefly explain vectors here.  Plenty of information out there on the web, and they are quite easy to understand.  Basically, a vector in computer graphics is an array of three numbers [X,Y,Z] that carry a direction and a magnitude.  The magnitude can mean a few different things, depending on context.  For instance, the magnitude can indicate the speed an object is traveling at, when talking about moving objects.  It can also indicate the distance from one point to another point (the components tell you which direction to travel to reach that point).

There’s a formula for calculating the magnitude of a vector, and I will show a couple ways of implementing this formula.

The basic formula is:

Given vector [X, Y, Z], the magnitude is the square root of the dot-product of the vector with itself.

√(X^2 + Y^2 + Z^2)

I won’t get into what a dot-product is here, but let’s just say that this formula works.

So, how does this give us distance?

Consider two points in space, PointA with coordinates (X, Y, Z) and PointB with coordinates (A, B, C).  To get the distance between these points we get the difference between each component and create a new vector with that information, then plug it into our magnitude formula, which will spit out a scalar number (A number with only one component, as opposed to our vector, which has three).

So, our distance vector is: [A-X, B-Y, C-Z]

The magnitude of this is: √[(A-X)^2 + (B-Y)^2 + (C-Z)^2]

Written as a dot-product, if [A-X, B-Y, C-Z] = Vector V,  the magnitude is: √(V•V)

These two diagrams also illustrate two ways of calculating distance. Since most computer programs and computing languages already have functions to calculate dot products, you’ll see you can do this quicker with less nodes/code.